二、圆柱拉、压螺旋弹簧的设计约束分析
1、强度约束条件
图12-6为承受轴向载荷的压缩弹簧,现分析其受力情况,拉伸弹簧的簧丝受力情况完全相同。如图12-6a,在通过轴线的剖面上,弹簧丝的剖面为椭圆,但由于螺旋升角一般很小,可近似地用圆形剖面代替。将作用于弹簧的轴向载荷F移至这个剖面,在此剖面上有转矩:T=FD2/2和剪切力F的联合作用。这二者在弹簧丝剖面上引起的最大剪切应力τ为:
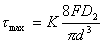
式中:K为曲度系数(或称补偿系数),用以考虑螺旋升角和弹簧丝曲率等的影响,其值可按下式计算:
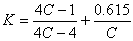
则弹簧丝的强度约束条件为:
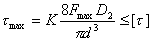
或
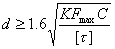
式中:[τ]为许用剪切应力;
Fmax为弹簧的最大工作载荷。
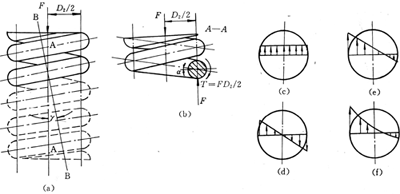
图12-6 受轴向载荷的压缩弹簧
2、刚度约束条件
圆柱螺旋弹簧的变形计算公式是根据材料力学求得的,即:
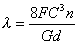
式中,G为材料的剪切弹性模量。由此可得刚度约束条件为
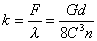
或
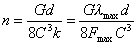
式中:k为弹簧刚度,表示弹簧单位变形所需的力。
一般n应圆整为0.5的整数倍,且大于2。
3、稳定性约束条件
当作用在压缩弹簧的载荷过大,高径比b=H0/D2超出一定范围时,弹簧会产生较大的侧向弯曲(图12-7)而失稳。
为保证弹簧的稳定性,一般规定,两端固定时取b<5.3;一端固定另一端自由时,取b<3.7;两端自由时,应取b<2.6。如未能满足上述要求,则要按下式进行稳定性验算:
Fmax<FC=CBkH0
式中:FC为临界载荷,CB为不稳定系数,见图12-8。
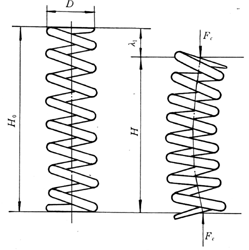
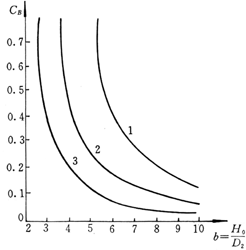
图12-7 压缩弹簧的失稳 图12-8 不稳定系数CB